Understanding bond risk is essential for making sound investment decisions—especially when interest rates are changing. One of the most powerful tools for measuring a bond’s sensitivity to interest-rate movements is Macaulay Duration. Although often overlooked by beginners, duration is a core concept used by professional analysts, fixed-income managers, and institutions to manage risk and compare bonds accurately.
In this guide, we explain what Macaulay Duration is, why it matters, how to calculate it, and how it differs from Modified Duration and Effective Duration. At the end, you will find a link to our free Macaulay Duration & Modified Duration Calculator, which performs the calculations instantly.
Macaulay Duration represents the weighted average time it takes to receive all cash flows from a bond—both coupon payments and the final principal repayment. In other words, it tells you how long, on average, it takes for the investment to “pay back” its cost.
Duration is expressed in years, and it is usually shorter than the bond’s maturity unless the bond is zero-coupon.
It measures the time-weighted present value of each cash flow.
Macaulay Duration is not just about time—it is directly linked to interest-rate risk, which makes it essential for fixed-income strategy and portfolio construction.
Macaulay Duration helps investors and analysts:
Bonds with higher duration lose more value when interest rates rise.
Two bonds with similar maturities can have vastly different durations due to coupon levels and yields.
Duration matching is widely used to hedge interest-rate risk.
Because Macaulay Duration reflects weighted cash-flow timing, it provides a realistic view of long-term sensitivity—not just nominal maturity.
The formula incorporates every future cash flow, discounted back to today’s value:
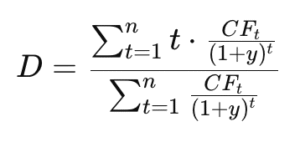
Where:
t – time in years to each cash flow
CF – each coupon or principal cash flow
y – yield to maturity
n – coupon frequency
This calculation is complex and nearly impossible to do manually for bonds with irregular coupon schedules or non-annual frequencies. That’s why most investors rely on calculators.
Consider a bond with:
Face value: $1,000
Coupon rate: 5% annually
Yield to maturity: 4%
Maturity: 5 years
Even without calculating manually, we know:
Maturity is 5 years
Coupon > yield → duration will be below 5
Higher coupons shorten duration
A typical Macaulay Duration for this bond would be around 4.5 years.
This means the investor effectively recovers the cost of the investment after 4.5 years in discounted cash-flow terms.
While Macaulay Duration measures time, Modified Duration measures price sensitivity.
Modified Duration tells you how much the bond’s price will move for a 1% change in yield.
This is why investors typically use both metrics together.
Duration is especially relevant when:
Interest rates are volatile
You compare bonds with different coupon structures
You manage risk in a fixed-income portfolio
You anticipate central bank rate changes
You evaluate long-term positions
If you invest in bonds or plan to duration should always be in your analysis.
Instead of doing manual calculations, you can use our free:
Macaulay Duration & Modified Duration Calculator
Our tools compute:
Macaulay Duration
Modified Duration
Accrued interest
Dirty price
Yield-to-maturity values
All you need to do is input your bond details.
No. Duration accounts for discounted cash flows, while maturity is only the final payment date.
No. Duration is always positive.
No. Duration is always positive.
Yes. Because they pay only at maturity.
Yes. Because they pay only at maturity.