Understanding how a bond reacts to changes in interest rates is one of the most critical skills in fixed-income investing. While Macaulay Duration measures the weighted average time of cash flows, Modified Duration goes a step further — it quantifies how sensitive a bond’s price is to changes in yield. If you want to manage risk, compare bonds, or build an immunized portfolio, Modified Duration is a metric you cannot afford to ignore.
In this article, we break down what Modified Duration is, how it works, how it differs from Macaulay Duration, and why professional bond investors rely on it. You will also find a link to our free Macaulay & Modified Duration Calculator, which performs all calculations automatically.
Modified Duration measures the percentage change in a bond’s price for a 1% (100 basis point) change in yield.
It is derived directly from Macaulay Duration and incorporates the bond’s yield-to-maturity (YTM) to estimate interest-rate sensitivity.
The formula is:
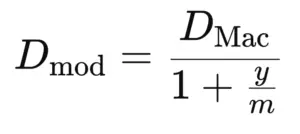
Where:
y = bond’s yield to maturity
m = compounding frequency (e.g., annual, semi-annual, quarterly)
If a bond has a Modified Duration of 7, then a 1% increase in yield will cause the bond’s price to fall by approximately 7%.
Conversely, a 1% decrease in yield will increase the bond’s price by roughly 7%.
It is a direct, intuitive measure of risk — the higher the Modified Duration, the more volatile the bond.
Modified Duration is essential for several reasons:
It allows investors to measure how much a bond’s value will change if interest rates rise or fall.
Professional asset managers match duration across portfolios to reduce interest-rate exposure.
Two bonds with identical maturities can have very different risks — Modified Duration reveals the difference.
When constructing barbell, bullet, or ladder strategies, duration is a core parameter.
Even though the two are closely related, they serve different purposes:
Concept | Measures | Used For | Unit |
|---|---|---|---|
Macaulay Duration | Time-weighted cash flow average | Cash-flow timing | Years |
Modified Duration | Price sensitivity | Risk analysis | % change per 1% yield |
In short:
Macaulay Duration = time
Modified Duration = risk
Most investors rely on Modified Duration for pricing impact and on Macaulay Duration for understanding cash-flow structure.
Macaulay Duration: 6.2 years
Yield to maturity: 4%
Compounded semi-annually
Modified Duration = 5.97
A 1% increase in rates → bond price falls ~5.97%
A 1% decrease in rates → bond price rises ~5.97%
This makes Modified Duration extremely valuable when evaluating market risk.
Calculating Modified Duration manually requires:
Full cash-flow schedule
Present value math
Yield compounding adjustments
Bond pricing logic
For bonds with semi-annual or quarterly coupons, irregular payment dates, accrued interest, or non-standard yields, manual calculation becomes impractical.
That’s why we built a tool that handles everything automatically.
Try the Macaulay & Modified Duration Calculator
The calculator computes:
Macaulay Duration
Modified Duration
—all instantly.
Modified Duration is especially useful when:
Assessing interest-rate sensitivity
Comparing bonds with different coupon structures
Evaluating long-term or volatile market positions
Managing fixed-income portfolios against benchmark duration
Implementing interest-rate hedging strategies
If you care about how much your bond’s value may swing with a rate hike or cut — Modified Duration is the metric you need.
Instead of doing manual calculations, you can use our free:
Macaulay Duration & Modified Duration Calculator
Our calculator computes:
Macaulay Duration
Modified Duration
All you need to do is input your bond details.
Yes, because it divides Macaulay Duration by (1 + YTM/m).
It works best for small rate changes. For larger moves, Effective Duration is more precise.
Yes, and Modified Duration = maturity ÷ (1 + YTM/m).
Correct. More cash paid earlier reduces sensitivity.